ÁNGULOS

Es la union de 2 semirrectas que se cortan en un punto . las 2 semirrectas se llaman lados del angulo y el punto en comun es el vertice.


 ÁNGULOS EN POSICIÓN NORMAL

un angulo que esta en posición normal o estándar . si esta representado en un sistema de coordenadas en el cual su vértice es el origen y su lado inicial coincide con el semi eje positivo  x .
la ubicación del lado final del angulo en posición normal permite determinar el cuadrante donde se encuentra el angulo.




MEDICIÓN DE ÁNGULOS EN EL SISTEMA SEXAGESIMAL

la unidad de medida de ángulos en el sistema sexagesimal es degradado cuando un angulo realiza una rotación completa , es decir , que el lado final coincide con el lado inicial el angulo se denomina angulo giro y su medida es de 360°





EJEMPLOS :
1) expresar 56,74° en grados °, minutos ',segundos".

56,74° →
= 56° + 0,74
=56°+(0,74) (60)
=56°+44,4
=56°+44'+04
=56° +44'+(0,4 . 60)
=56°+44'+ 24"
=56°,44',24"

ÁNGULOS COTERMINALES

• 2 ángulos de posición normal son coterminales si comparten el mismo lado final ,en este caso no importa la magnitud ,ni el sentido de la rotación de los ángulos . para encontrar ángulos que son coterminales un angulo teta en posición normal , se suma o se resta múltiplos de 360°

Por ejemplo, para encontrar ángulos que son coterminales con el angulo 0= 120° en posición normal, se suma o se resta múltiplos de 360° como sigue:

120° + 360°  = 480°  y  120° + 720° = 840°

Por lo tanto los ángulos 480° y 840° son coterminales con 0= 120°:

Los ángulos negativos son coterminales con 0= 120° se obtiene como: 

120°-360°=-240° y 120°-720°=-600°

Así los ángulos -240° y -600° son coterminales con 0= 120°

FUNCION DE ANGULOS EN EL SISTEMA CICLICO

La unidad de medida de ángulos en el sistema cíclico es el radian .La medida de un angulo en el sistema de un angulo en el sistema cíclico se determina aparir de la relación que existe entre un angulo central  en una circunferencia  con centro en el origen y radio . el angulo teta formado por 2 radios y el arco S cuyo vértice se el origen se denomina angulo central.

Cuando la medida del radio del arco es S , es la misma  medida del radio de la circunferencia se dice que teta mide un radian así, θ igual un radian de θ = r es la medida del angulo central teta cuyo arco mide 1 radio.

EJEMPLO:

LONGITUD DE ARCO
 para determinar la longitud de arco se considera  θ un angulo central medido en radianes que subtiene   de un arco de longiitud S , en la circunferencia de radio ., entonces , el angulo central  teta determina la longitud S que es una parte de la longitud de la circunferencia .

AREA DE SECTOR CIRCULAR

sesa θ angulo central medidda en radianes de una circunferencia de rardio r , y si a es el area del sector circular .
subtenido por teta entonces a=1/2 r ala 2 θ




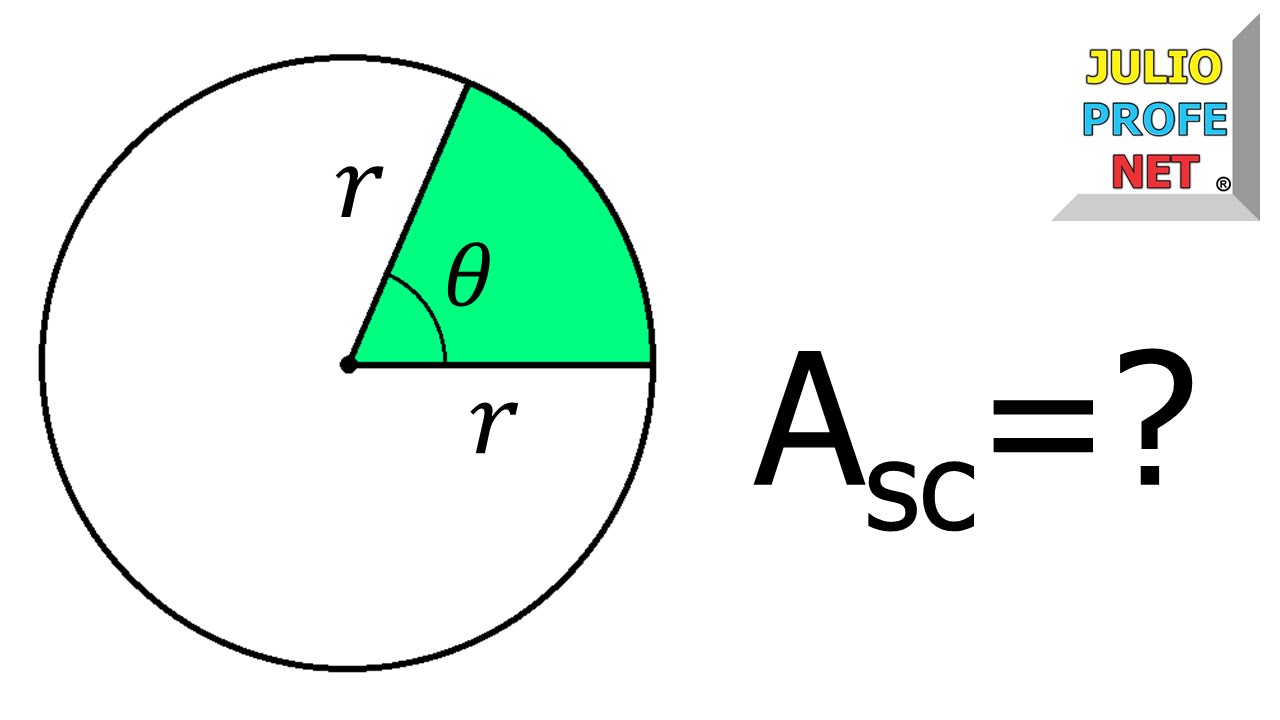
VELOCIDAD ANGULAR

cuando un cuerpo gira con rapidez constante formando un angulo central  θ , la velocidad angular  es la razon entre el angulo central recorrido durante cierto tiempo asi
w=θ/T

VELOCIDAD LINEAL

la velocidad lineal es la razon entre la longitud de arco rrecorrida y el tiempo que dura este recorrido.
V=S/T
 
V=θ /TV=W,r



TRIANGULOS



PROPIEDADES DE LOS TRIANGULOS

 los triangulos cumplen las siguientes propiedades

• la suma de las medidas de los angulos interiores de todo triangulo es 180° . todo triangulo equilatero es equiangulo es decir, las medidas de sus angulos internos son iguales , en este caso cada angulo mide 60°.

• si 2 lados de untriangulo tienen igual medida , entonces , los angulos opuestos a estos lados tambien son de igual medida.

•si 2 angulos de un triangulo tienen igual medida entonces, los lados opuestos a estos angulos tienen igual medida.

 TEOREMA DE PITAGORAS

BIOGRAFIA DE PITAGORAS DE SAMOS

La vida de Pitágoras se encuentra envuelta en leyendas. Nació en Jonia, en la isla de Samos, hacia el 572 a.C. y, al parecer, conoció a Anaximandro de Mileto. Se le atribuyen viajes a Egipto y Babilonia. La tiranía de Polícrates le hizo abandonar Samos, trasladándose a Italia y estableciéndose en Crotona. Allí creó una secta filosófico-religiosa, inspirada en el orfismo, cuyos miembros vivían en comunidad de bienes, participando de un conjunto de creencias y saberes que permanecían en secreto para los no iniciados.

La influencia ejercida por dicha secta en Crotona fue considerable, al parecer, llegando a suscitar la enemistad del pueblo que se rebeló contra el dominio ejercido por las secta pitagórica y, en el transcurso de esa revuelta popular, puso fuego a sus propiedades y los expulsó de la ciudad. Se dice que Pitágoras se refugió en Metaponto, donde murió poco después, hacia el 496 antes de Cristo.

• en todo triangulo rectangulo decatetos a y b e hipotenusa c , se cumple que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

RELACIONES RECIPROCRAS

sea p (x.y) el punto sobre la circunferencia unoitrua determinado por el angulo θ . a partir  de las definiciones de las funciones trigonometricas se obtienen las siguientes relaciones.

senθ= y

cosθ= x

tanθ= y/x

cotθ= x/y

secθ= 1/x

cscθ= 1/y

 FUNCIONES PARES E IMPARES

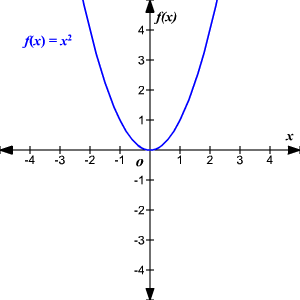
Una función es par si, para cada x en el dominio de f ,   f (– x ) = f ( x ).  Las funciones pares tienen simetría reflectiva a través del eje de las y .

Ejemplo de una función par:

   f ( x ) = x 2 
  f (– x ) = (– x ) 2 = x 2 = f ( x )

   

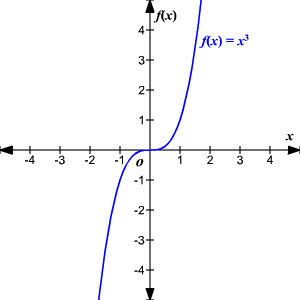
Un función es impar si, para cada x en el dominio de f ,  f (– x ) = – f ( x ).  Las funciones impares tienen simetría rotacional de 180º con respecto del origen.    

Ejemplo de una función impar:

    f ( x ) = x 3 
f (– x ) = (– x ) 3 = – x 3 = – f ( x )